Most egy laza balkanyarral elugranék egy teljesen más téma irányába. Eddig az adathalmazok középértékeivel és szóródásával foglalkoztam, de most egy könyv olvasása során felkeltette az érdeklődésemet az extrém szélsőséges események előfordulási valószínűségeinek vizsgálata – legalábbis egy bejegyzés erejéig. Az extrém szélsőséges események – legyenek azok időjárási vagy természeti jelenségek vagy gazdasági események – hajlamosak súlyos következményekkel járni, mert ezekre általában nem vagyunk felkészülve.

A problémát a következő kérdéssel lehet megvilágítani: Vajon mekkora az évszázad áradása egy folyón. Ami természetesen egy fontos kérdés, hiszen úgy érdemes megépíteni a gátakat és kialakítani az árvízvédelmi rendszert, hogy lehetőleg még az évszázad árvize esetén is védelmet nyújtson. De hogy találjuk ki, hogy milyen magas lesz a vízállás az évszázad árvizekor, ha egyszer ez csak 100 évenként egyszer fordul elő? Még ha a rendelkezésünkre is állna az adatsor, ami az elmúlt 100 év legmagasabb vízállásait tartalmazza, akkor is honnan tudjuk, hogy az évszázad árvize már előfordult, és nem lesz még ennél is nagyobb katasztrófa a jövőben?

Először egy Leonard Henry Caleb Tippet nevű tudós foglalkozott ezzel a kérdéssel, aki egy teljesen más témával kapcsolatban dolgozta ki az első elméletet. Tippet úr a British Cotton Industry Research Lab-nél, vagy ahogyan akkoriban hívták, a Shirley Institute-nál dolgozott és a pamutfonalak erősségét vizsgálta. Arra jött rá a fonalak mikroszkópos vizsgálata során, hogy a szakadáskor a fonat leggyengébb szála szakad el először. De melyik a leggyengébb szál? Hogyan lehet matematikai módszerrel modellezni a leggyengébb szálat? Ezt a kérdést Tippet végül Ronald Fischer segítségével tudta megoldani.

Végül 1958-ban Emil Julius Gumbel publikálta a módszert a „Statistics of extremes” című tanulmányában, amely végül alapja lett a jelenleg alkalmazott módszereknek. A Gumbel által kidolgozott eloszlást becézik Gumbel eloszlásnak, de találkozni lehet még a Log-Weibull, a Gompertz, a Fischer-Tippett valamint az „Extreme Value Type I” elnevezésekkel is, csak hogy az élet egyszerű legyen. Napjainkra az alkalmazott statisztikai eszközök tárháza igen bőségessé vált, így nem is szeretném felvállalni azt, hogy mélyebben belemegyek a téma ismertetésébe. A bejegyzés terjedelme és a saját befogadóképességem korlátai miatt is inkább csak a Gumbel által kidolgozott megközelítést szeretném bemutatni egy példán keresztül.

A mai példám arról szól, hogy 2000 január 25-én rekord mennyiségű (20,3 hüvelyk, azaz 51 cm) hó zúdult az Észak-Karolinában található Raleigh-Durham reptérre, megbénítva a reptér forgalmát, illetve a környék energiaellátását és a helyi iskolák és munkahelyek életét is.

A súlyos következménnyel járó időjárási jelenségről szóló újságcikkek kiemelték, hogy ehhez hasonló mértékű hóesés csak 100-200 évenként egyszer fordul elő. Esetünkben a probléma felvetése az, hogy a múltbeli adatok alapján mennyire lehetséges megjósolni egy ilyen extrém időjárási jelenség bekövetkezésének valószínűségét.

A vizsgálatunkhoz felhasznált adatsor a környéken 1948 és 1998 között minden év január hónapjában leesett legtöbb hó mennyiségét tartalmazza:

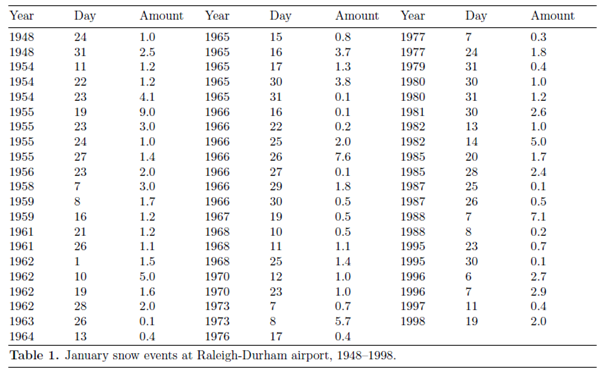
Mielőtt azonban belefognék az elemzés elkészítésébe és a fent megfogalmazott kérdés megválaszolásába, tennék még egy kis kitérőt és általánosságban elmerülnék az extrémérték-elmélet alapjainak megértésében.

Korábban már foglalkoztunk azzal, hogy egy adott sokaságból kivett minták középértéke hogyan viselkedik és milyen eloszlást követ (A nagy dobókocka kísérlet), de azt még nem vizsgáltuk, hogy a minták szélsőértékei (legkisebb vagy legnagyobb elemei) vajon milyen eloszlást követnek. Ismételten tartózkodnék a száraz elméleti leírásoktól, inkább megint elkezdtem játszani a táblázatkezelővel és szimulálni a jelenséget. Most nem dobókocka dobásokat vizsgáltam, hanem készítettem egy 10 000 elemből álló standard normál eloszlású sokaságot (Első az egyenlők között – a standard normál eloszlás). A sokaság legkisebb értéke -4,44, a legnagyobb érték pedig 4,04. Ebből a sokaságból véletlenszerűen kiválasztottam 1000 darab 500 elemű mintát. Eddig ez nagyon hasonlít a korábbi dobókockás elemzéshez, itt azonban nem a minták átlagát számoltam ki, hanem kiválasztottam minden egyes mintából az 500 elem közül a legnagyobbat.

A kapott 1000 darab számot egy hisztogramon ábrázoltam:

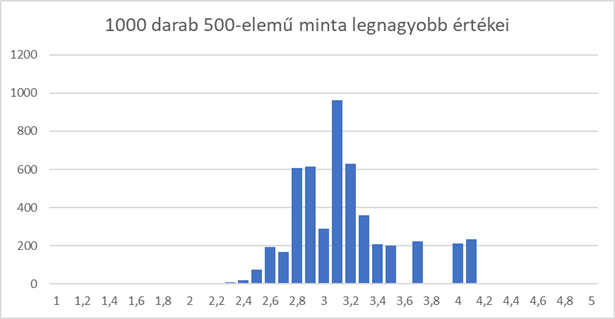
Első ránézésre a hisztogram olyan, mintha egy aszimmetrikus eloszlás lenne, vagyis mintha itt nem érvényesülne a Centrális Határeloszlás tétele. És tényleg; Gumbel is azt találta, hogy a minták maximális értékei esetében az eloszlás balra dől és a jobb oldali „farka” hosszabb, mint a bal oldali (csak mellékesen jegyzem, meg, hogy a minták minimális értékei esetében ez pont fordítva van, vagyis az eloszlás jobbra dől és a bal oldali vége hosszabb). A fenti hisztogramon még az is megfigyelhető, hogy a vízszintes tengelyen 2,3 a legkisebb érték, amely már előfordult a minták maximumai között és még 4 feletti értékek is vannak az 1000 darab szám között, ami azért meglepő mert a 10 000 darabos sokaságban összesen kettő darab 3,9-nél nagyobb érték található.

Mivel a minták 500 elemből állnak, ezért a jelenség nem meglepő, a minta maximumok körülbelül ebbe a tartományba esnek.

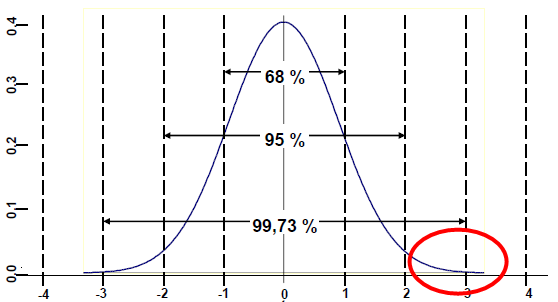
Jó, de akkor milyen eloszlás alapján, illetve milyen sűrűségfüggvény segítségével tudjuk megbecsülni egy adott érték, vagy annál nagyobb érték előfordulási valószínűségét? Nos, Gumbel a következő függvényképletet adta meg a szélsőértékek becslésére:

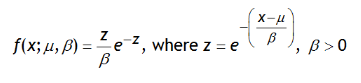
Jó, ez most megint nagyon érthetetlenül néz ki, én is néztem bután, hogy ezt akkor most hogyan is kell használni. Ráadásul ennek a függvénynek – a normál eloszláshoz hasonlóan – van két paramétere, amelyet meg kell határozni, nyilvánvalóan a minta alapján. Mellékesen jegyzem meg, hogy még a hozzáférhető komoly szakirodalomban sem mindenütt hibátlan a képlet, sajnos több helyen is azt tapasztaltam, hogy a Z értékének meghatározásakor az e kitevőjében szereplő képlet elől hiányzott a mínusz-jel és úgy a függvény nem működik helyesen (kipróbáltam!).

De vissza az előző kérdéshez: mit jelent a µ és β a fenti képletben? A hozzáférhető irodalom ismételten különféle megközelítéseket ismertet. Az egyik helyen azt írták, hogy µ az adatsor móduszát jelenti, a másik helyen a minta átlagából kellett kivonni β-nak az Euler-féle számmal módosított értékét. A β-val kapcsolatban szintén csak abban egyeztek meg a különféle források, hogy ezt az adatsor szórása alapján kell kiszámítani, de a vélemények itt is megoszlottak.

A vicces az, hogy a sokféle variáció kipróbálása után arra a következtetésre jutottam, hogy a legjobb közelítést az adta, ha µ helyére az adatsor átlagát, β helyére pedig az adatsor szórását helyettesítettem be. Ez lehet, hogy amiatt van, mert a sokaság normál eloszlású, de az is lehet, hogy más az ok, de így működött a legjobban.

Vagyis először vettem az 1000 darab minta legnagyobb értékeit és kiszámítottam ezek átlagát és szórását. Ezután létrehoztam egy táblázatot, amelyben kiszámoltam az egyes x-értékekhez tartozó F(x) függvényértékeket:

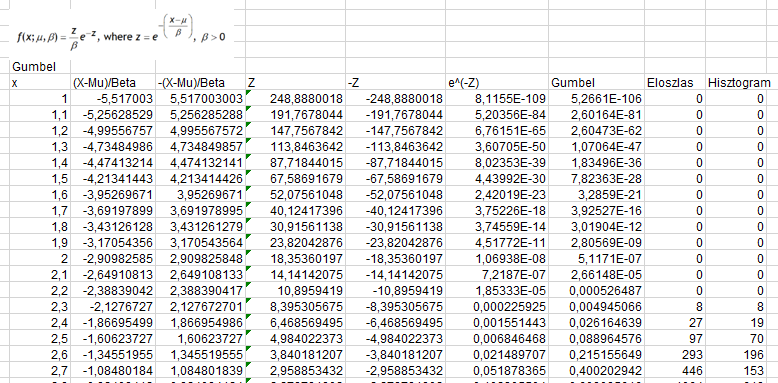
A legelső oszlop tartalmazza a Z-értékhez tartozó kitevő számítását, a harmadik oszlopban ezt megszorzom -1-gyel, majd a negyedik oszlopban kiszámítom Z értékét. Az ötödik oszlopban ezt ismét megszorzom -1-gyel, majd a hatodik oszlopban kiszámítom az e a mínusz Z-ediken tagot. Az utolsó lépésben már csak ezt kell megszorozni a Z/β hányadossal, és már kész is a mutatvány. Innen nézve már nem is tűnik annyira bonyolultnak a történet, csak első ránézésre ijesztő a képlet.

Már csak össze kellett gyógyítani a hisztogramot a függvénygörbével és kész is a burkoló görbe. Nem olyan szép, mint az elmélet, de rá lehet fogni.

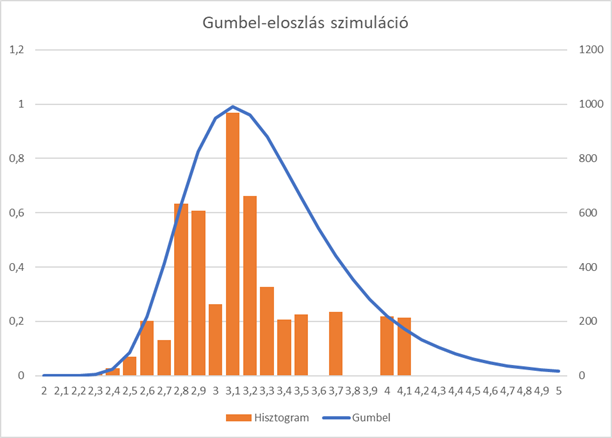
És akkor most vissza a hóviharhoz.

A fentihez hasonlóan elkészítettem a januári havazások elemzését, hogy megtudjam, mekkora a valószínűsége annak, hogy fél méter hó esik a környéken. A teljes táblázat így néz ki:

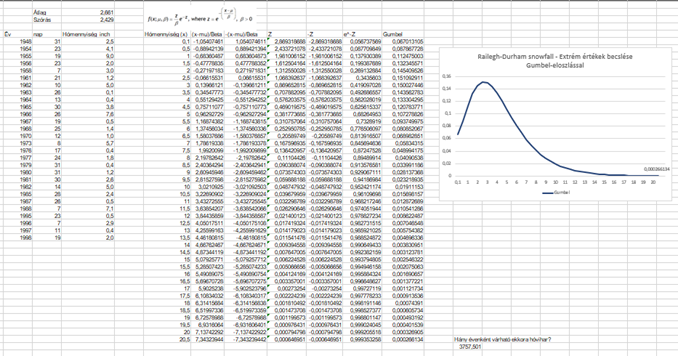
Először minden évből kiválasztottam azt a napot, amelyiken a legtöbb hó esett. Így minden évre egy érték jut. Ennek az adatsornak kiszámoltam az átlagát és a szórását, majd az egy napra eső hómennyiséget vettem x értékének, hiszen arra vagyok kíváncsi, hogy mekkora a valószínűsége annak, hogy 20,3 hüvelyknyi hó fog esni. Ehhez a fentihez hasonló módon kiszámoltam a Gumbel-eloszlás értékét minden x-re:

...

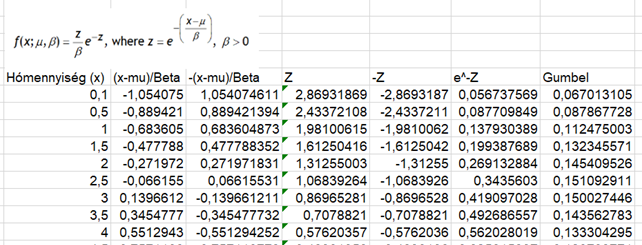
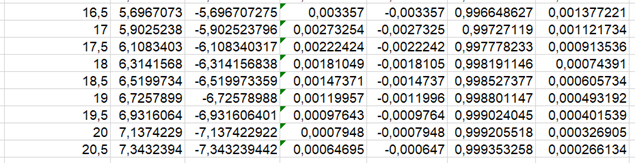
Végül a Gumbel-eloszlás értékeit egy grafikonon ábrázoltam, ahol a vízszintes tengelyen van a napi hómennyiség, a függőleges tengelyen pedig annak a valószínűsége, hogy ennyi hó fog esni:

Jól látható, hogy a 20 hüvelyknél nagyobb hó valószínűsége elenyésző, a becslés alapján kb. 0,026%. Ha ennek a számnak a reciprokát vesszük, akkor megkapjuk, hogy körülbelül 3700 évente egyszer fog ennyi hó leesni a környéken – figyelembe véve a történeti adatokat. Persze azt a kérdést is fel lehet tenni, hogy mekkora hó fog esni 100 évenként egyszer, hiszen a diagramról, illetve a fenti táblázatból ez is kiolvasható. Nos ez alapján 100 évenként egyszer fog 11,5 hüvelyknyi, azaz 28 cm hó esni.

Összegzés:

Nyilvánvaló, hogy az extrémérték-elmélet a fenti kis ujjgyakorlatnál sokkal többet jelent, de ez a kis játék talán jó volt arra, hogy megértsük a vizsgálat célját és elméletét. Akit jobban is érdekel, ez alapján már el tud indulni a komolyabb és modernebb elemzések irányába.

Források

David Salzburg: The Lady tasting tea, Henry Holt and Company, LLC, 2002

https://abc11.com/weather/raleigh-durham-area-sees-entire-winter-average-in-one-day/4866428/

https://www.newsobserver.com/news/weather/article125059664.html

https://projects.ncsu.edu/atmos_collaboration/nwsfo/storage/cases/20000125/

Statisztical Analysis Handbook 2018 edition – Gumbel and extreme value distribution
https://www.statsref.com/HTML/index.html?gumbel_extreme_value_distribut.html

Richard L. Smith: STATISTICS OF EXTREMES, WITH APPLICATIONS IN ENVIRONMENT, INSURANCE AND FINANCE, Department of Statistics, University of North Carolina, Chapel Hill, NC 27599-3260, USA – 12 March 2003
https://rls.sites.oasis.unc.edu/postscript/rs/semstatrls.pdf