
A címválasztás nem véletlen. Ez a latin kifejezés több szempontból is telitalálat a következő cikk témájával kapcsolatban. Az egyik ok az, hogy noha ez az Amerikai Egyesült Államok egyik első és nagyon híres jelmondata, amely egyébként a különféle dollár bankjegyeken és a váltópénzeken is szerepel, nem biztos, hogy sokan emlékeznek rá, hogy mit is jelent. A másik okom pedig a kifejezés jelentése volt, ugyanis a cikk témájául választott Hotelling T2-szabályozó kártya pontosan ezt teszi: Sok SPC-kártyából csinál egyet!
A probléma felvetése nem teljesen új, mint ahogy maga az eszköz sem, napjainkban azonban különleges jelentőséget ad ennek az Ipar 4.0 egyre erősebb jelenléte a gyártásban. Az Ipar 4.0 előretörése magával hozta többek között a gyártási folyamatok egyre magasabb fokú automatizálását és ezzel párhuzamosan a különféle érzékelők és jeladók elterjedését a gyártóeszközökben. Ezek az érzékelők és jeladók egyre több adatot szolgáltatnak a szakembereknek, akik eddig ki voltak éhezve a gyártásból érkező adatokra, mostanra viszont már annyira sok adat keletkezik, amelynek a feldolgozása meghaladja a szakemberek teljesítőképességét. A keletkezett adatok jelentős részére senki még csak rá sem néz. Hasonló jelenség zajlott le az 1990-es és 2000-es években a statisztikai folyamatszabályozó kártyák terén. Ahogy egyre bonyolultabbak lettek a gyártott termékek és egy-egy terméknek egyre több tulajdonságát kellett szigorú ellenőrzés alatt tartani, amelynek következtében akár több száz statisztikai szabályozó kártyát kellett volna követni és reagálni ezek jelzéseire. Mivel ez bőven meghaladja a gyártással foglalkozó szakemberek rendelkezésre álló kapacitásait, ezért napjainkra a statisztikai folyamatszabályozás gyakorlatilag elhalt, a vállalatok 90%-a csak passzív adatgyűjtést végez, az adatok feldolgozására, értelmezésére és ezek alapján a gyártási folyamatokba történő beavatkozásra már nem marad idő és energia.
Erre a problémára jelenthet megoldást a fentebb említett, Harold Hotelling matematikus által 1947-ben publikált T2 (T-négyzet vagy T-squared) statisztikai szabályozó kártya. Tulajdonképpen mit tud ez a kártya? Mitől olyan különleges, hogy érdemes cikket is írni róla? A legfontosabb képessége az, hogy ha van egy jelenség, dolog vagy folyamat, amelyet olyan formában figyelnünk meg, hogy folyamatosan vagy rendszeres időközönként a legkülönfélébb adatokat gyűjtjük össze róla, akkor
„ezeket az adatokat megfelelő módon szintetizálva képes minden egyes megfigyelést egyetlen számba sűrítve képes egy egyszerű statisztikai szabályozó kártya segítségével megmondani, hogy az adott megfigyelés véletlenszerűen történt, vagy a jelenség, folyamat vagy dolog valami miatt megváltozott”
A módszer megértéséhez szükséges a jelenségek vagy folyamatok véletlenszerűségének a megértése (Milyen eloszlást követ a barackmag tömege?), mert amikor eljutunk oda, hogy a p számú különféle jellemzőt egyetlen számmá sűrítjük, akkor onnantól a klasszikus egyváltozós statisztikai folyamatszabályozás törvényszerűségei fognak érvényesülni. De hogyan jutunk el a p darab jellemzőtől – azaz tulajdonképpen a p-dimenziós térből – oda, hogy azt egyetlen számmá tudjuk leképezni? Egyáltalán miért hívom a p különféle jellemző által definiált teret p-dimenziós térnek?
Nos, gondolkodjunk el egy kicsit. Ha a vizsgált jelenségnek csak egyetlen tulajdonságát vizsgálom, akkor az adott tulajdonsághoz hozzárendelt számszerű értékeket egy számegyenesen tudom ábrázolni. A vizsgált egyedeket aszerint tudjuk jellemezni, hogy mekkora a vizsgált tulajdonság távolsága az egyes egyedek esetében. Ha a két egyed távolsága a számegyenesen egy adott távolságon belül van, akkor adott valószínűséggel feltételezhetjük, hogy a két egyed ugyanahhoz a sokasághoz tartozik. Ha ez a távolság nagyobb egy adott értéknél, akkor viszont feltételezhetjük, hogy a két egyed NEM ugyanahhoz a sokasághoz tartozik. A célunk az, hogy időben észleljük, ha két egyed nem ugyanahhoz a sokasághoz tartozik, azaz a folyamatban valami megváltozott.
Ha a jelenséget két különböző tulajdonsága alapján vizsgáljuk, akkor egy kicsivel bonyolultabbá válik két egyed „távolságának” kiszámítása, de ha ez sikerül, akkor erre a kétdimenziós távolságra ugyanúgy igaz lesz a fent említett szabály, tehát ha a pontok kétdimenziós távolsága belül van egy megadott távolságon, akkor feltételezhetjük, hogy a két pont azonos sokaságból származik, míg a túl nagy távolság természetesen arra utal, hogy a két egyed nem ugyanoda tartozik. Ezt a távolságot a legegyszerűbb módon Pitagorasz-tétele alapján lehet meghatározni.
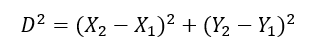
illetve
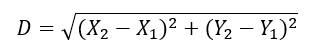
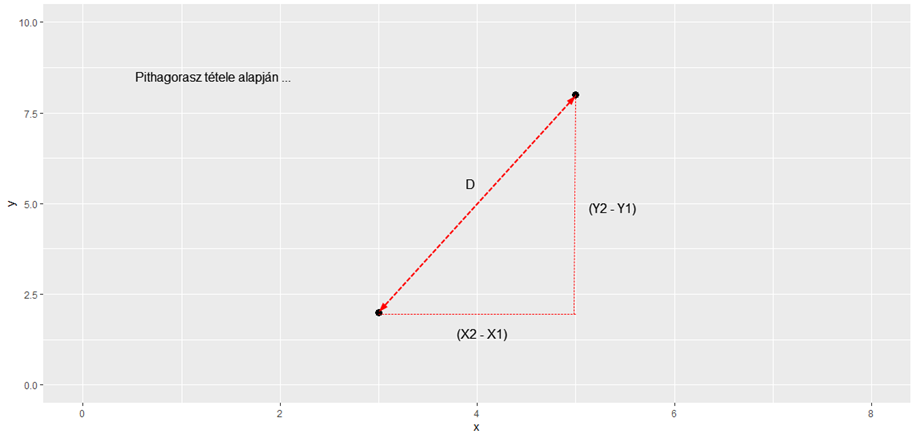
Háromdimenziós térben ez még eggyel bonyolultabb, de nem sokkal, csak annyival, hogy bejön egy harmadik változó.
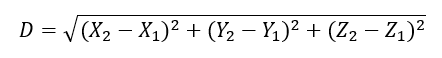
És ez akárhány tulajdonság vagy dimenzió esetében működik annak ellenére, hogy három dimenzió felett nehezen tudjuk ezt térben elképzelni vagy ábrázolni. Ezt a fajta távolságot két pont között Euklidész-i távolságnak hívjuk és ezt a fajta távolság értelmezést egyébként jó néhány gépi tanulási algoritmus is alkalmazza, például a ’kmeans’-algoritmus is (Tanítsuk a gépet klaszterezni! – A ’kmeans’-algoritmus).
Annak ellenére, hogy ez a távolság értelmezés közel áll az emberi gondolkodáshoz, könnyen el tudjuk képzelni, hogyan működik, mégis csak van vele egy apró probléma. Mégpedig az, hogy
„több jellemző vizsgálata esetében a jellemzők lényegesen különbözhetnek egymástól, ezért a fenti módon kiszámolt távolságok erősen torzulhatnak. Az adatok statisztikai jellegű feldolgozására ez a fajta távolság nem igazán alkalmas.”
Mi lenne, ha a különféle tényezőket közös alapra hoznánk és így összehasonlíthatóvá válnának? Erre láttunk már megoldást korábban, a standard normál eloszlás esetében (Első az egyenlők között – a standard normál eloszlás), amikor standardizálás segítségével bármilyen normál eloszlást visszavezettünk az egyetlen és megismételhetetlen standard normál eloszlásra. Ezt a módszert akár a pontoknak az átlagtól mért távolságának meghatározásakor is alkalmazhatnánk:
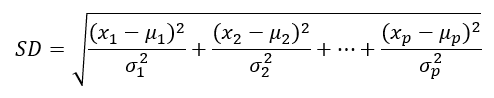
ahol SD a pontnak az átlagtól mért statisztikai távolsága,
x1..xp az adott megfigyelés i-dik tényezőjének mért vagy megfigyelt értéke,
μ1..μp az i-dik vizsgált tényező átlagértéke,
σ1..σp az i-dik vizsgált tényező szórása,
p pedig a vizsgált jellemzők száma.
Amint azt láthatjuk, a standardizálást „beloptuk” a távolságszámítás képletébe, így létrejött egy olyan távolságértelmezés, amely statisztikai szempontból sokkal jobban értelmezhető. Ráadásul ez a fajta eljárás sem teljesen új a hűséges blog olvasók számára, hiszen a korrelációs együttható kiszámításakor ezt a „trükköt” már alkalmaztuk egyszer (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?). A dolog lényegét egy kicsit más módon magyarázva annyit tettünk, hogy a különböző mértékegységekben mért jellemzők értékeit egy közös „mértékegységre” hoztuk, ez a mértékegység az „1 szórás”. Ezt a fajta távolságot is gyakran alkalmazzák a különféle gépi tanulási módszerek esetében, de ott ezt nem statisztikai távolságnak, hanem Mahalanobis-távolságnak becézik.
A cikk elején említettem, hogy a célunk tulajdonképpen az, hogy különbséget tegyünk azon pontok között, amelyeket ugyanabból a sokaságból, és azok között, amelyeket egy már megváltozott sokaságból vettünk ki. Ehhez viszont szükségünk lesz egy határértékre, amely a Z-próbához és a t-próbákhoz hasonlóan megmondja, hogy mekkora az a távolság, amelynek esetében mondjuk 95%-os valószínűséggel állíthatjuk, hogy amennyiben a pontok ennél közelebb vannak a pontok átlagához, akkor nincs bizonyítékunk arra, hogy ezek különböző sokaságokból származnak, azaz feltételezzük, hogy ugyanabból a sokaságból vettük ki őket.
Persze ez esetben a sokdimenziós pontok átlaga is érdekesen értelmezhető, hiszen az átlag maga is egy pont lesz az 'n-dimenziós' térben, amelynek dimenzióit úgy kapjuk meg, hogy az adathalmazunk pontjainak összes dimenzióját átlagoljuk. Tegyük fel, hogy van három pontunk és mindegyiknek van három dimenziója:

Ekkor a három pont átlaga maga is egy háromdimenziós pont lesz, amelynek az első dimenziója (8 + 4 + 6) / 3 = 18 / 3 = 6 lesz. A másik két dimenziója hasonló módon számolódik ki.
Ez így elsőre még akár egyszerűnek is tűnik, de azért a dologban még van egy kis csavar. Mivel egy olyan rugalmas rendszerről beszélünk, amelyben nincs rögzítve a vizsgált tényezők, illetve egyedek száma, ezért a fent említett távolságok kiszámítása sajnos nem ennyire egyszerű. Az említett rugalmassági feltétel miatt a pontoknak az átlagtól való távolságát különféle mátrixműveletek segítségével tudjuk meghatározni, amelyeket kézzel elvégezni nem lehetetlen, de meglehetősen időigényes feladat (még táblázatkezelő segítségével is), ezért ebbe most nem szeretnék részletesen belemenni. Emiatt a módszer alkalmazásához sajnos célszoftverre van szükségünk. Ez lehet a fizetős Minitab, de akár az ingyenes R-ben is megvalósítható egy ilyen alkalmazás. Ha csak magára a T2-kártyára vagyunk kíváncsiak, akkor ezt R-ben az 'iqcc' csomagban található két függvény alkalmazásával is megtehetjük.
Az 'n-dimenziós' térben ugyanúgy ki lehet számolni, mint egy hagyományos „egydimenziós” SPC-kártya esetében, csak persze ez esetben egy sokkal bonyolultabb kalkuláció szükséges ehhez. Van még néhány előfeltétel a kiinduló adatokkal kapcsolatban. Például amikor két tényező között nagyon szoros összefüggés van, azaz a köztük lévő korrelációs együttható értéke nagyon közel van 1-hez vagy -1-hez, akkor az úgynevezett kollinearitás jelensége lép fel, azaz a modell „túlhatározottá” válik, így az eredmények torzulnak. Hasonlóképpen vizsgálnunk kell az autokorreláció (Autokorreláció – Mennyire függ a jövő a múlttól?) jelenségének előfordulását is, mert ez pedig fals hibajelzéseket eredményezhet.
De hagyjuk az elméletet, inkább mutatok egy példát arra, hogy mire jó ez az egész. Találtam egy olyan adatsort, amely egy termék különböző tulajdonságait vizsgáló próbapadból származik. A próbapad a termékek 13 különféle tulajdonságát vizsgálja meg. Az adatsor 66 darab termék mérési eredményeit tartalmazza. Az alábbi táblázat az eredmények egy részletét mutatja be.
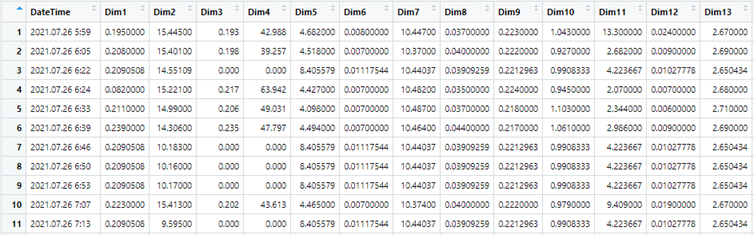
Ha a hagyományos módon szeretnénk az egyes jellemzők stabilitását megvizsgálni és nyomon követni, akkor 13 statisztika szabályozó kártyát kellene rendszeres időközönként megvizsgálnunk, amely azért egy eléggé időigényes és fáradtságos művelet lenne. A 13 jellemző értékeit összekombinálva azonban egyetlen Hotelling T2-kártya segítségével teljes egészében áttekinthetjük a gyártási folyamat egészét!
Végül én magam készítettem el azt a programot, amely az alábbi diagramot megrajzolta:
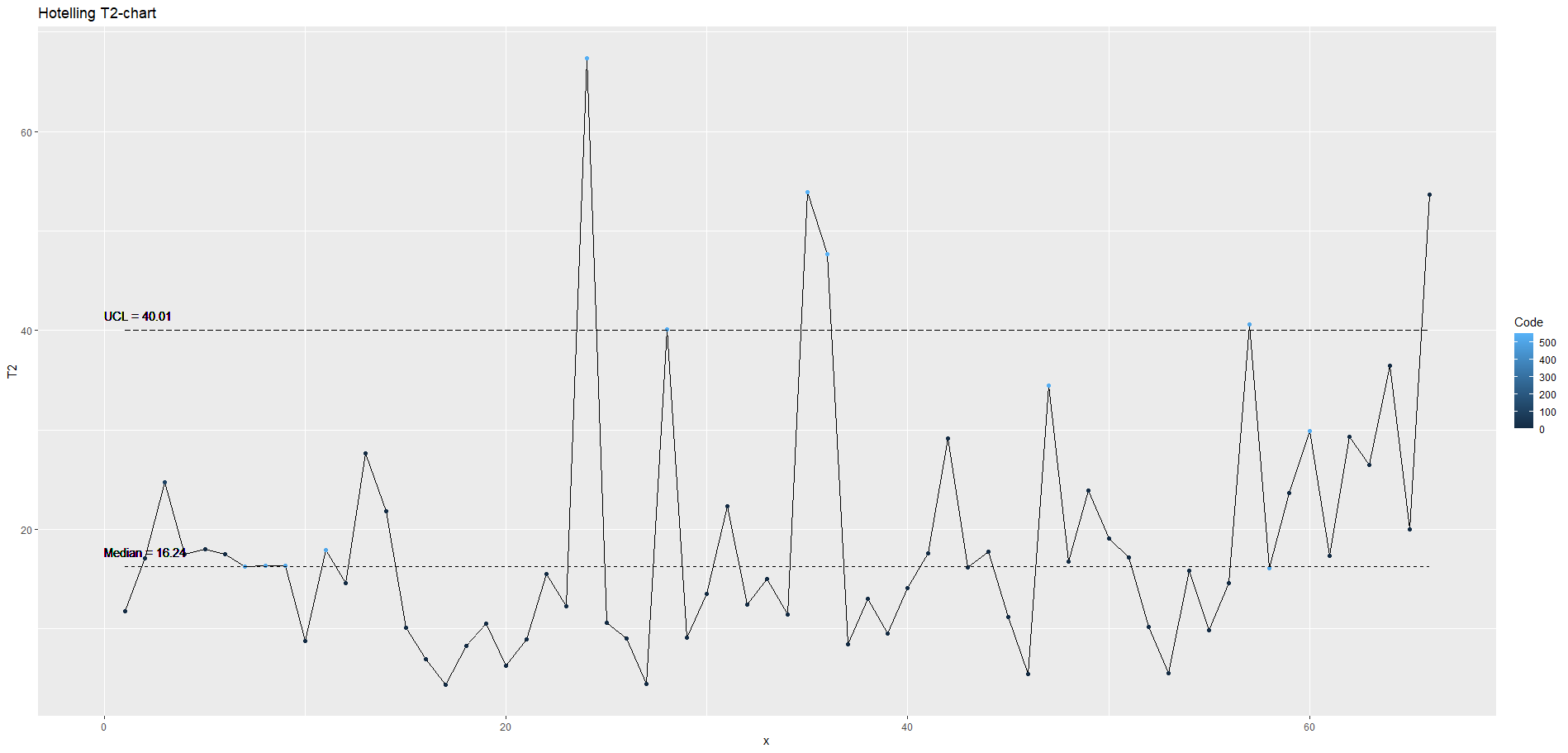
A kártyáról szépen leolvasható, hogy a műszak első harmadában még stabil volt a gyártás, attól kezdve viszont valami megváltozott, amely a mért értékek szórásának lényeges növekedését eredményezte. A felső diagramon az UCL vonal (az ábrán a szaggatott vonal) feletti értékek ezt világosan jelzik. Ha a csoportvezető vagy a minőségügyi mérnök ezt érzékelte volna a szabályozó kártya alapján, akkor még időben közbe lehetett volna avatkozni a veszteségek csökkentése érdekében.
Az adatok értelmezése így egyszerűnek tűnik, azonban amikor sokdimenziós adathalmazokat vizsgálunk, akkor egy-egy beavatkozási határon kívül eső pontnál kihívást jelenthet megtalálni azokat a dimenziókat, amelyek megváltozása miatt a pont a beavatkozási határon kívülre került. Erre is van megoldás, de ezt egy másik cikkben fogom ismertetni valamikor a következő hetekben.
…és itt jöhetne a klasszikus idézet, hogy „I have a dream!”, azaz van egy álmom. A mai ipar körülményei között kivitelezhetetlennek tartom, hogy egy termelő üzemben, ahol akár sok tucat gyártóeszközön keletkező sok ezer adatot valakik folyamatosan figyeljék és beavatkozzanak a gyártási folyamatba, ahol és amikor szükséges. Annak viszont igenis látom realitását, hogy minden gyártóeszköz mellett vagy felett legyen egy monitor, ahol az adott eszköz által működtetett szenzorok és mérőeszközök által szolgáltatott adatoknak a fenti módon összekombinált eredményei egyetlen Multivariate SPC kártyán megjelenjenek és folyamatosan frissüljenek, ahogy az újabb és újabb darabokat ellenőrzi a folyamat. Ugyanígy lehetségesnek tartom, hogy a rendszer valamilyen üzenetet küldjön a felelős gyártómérnököknek, ha valami történik a folyamatban és emiatt elemzés és beavatkozás szükséges. Egy ilyen rendszer nagymértékben javítaná a minőséggel kapcsolatos történések átláthatóságát és a gyorsabb beavatkozások által csökkentené a veszteséget. A Hotelling T2-kártyával kapcsolatos szakirodalom ráadásul egyszerű megoldási javaslatokat kínál a bevezetés során felmerülő kérdések jelentős részére, például az adatokból hiányzó értékek kezelésére is, amely szintén abba az irányba mutat, hogy a módszer alkalmas lehet a gyártásban keletkező adatok látványos feldolgozására.
Persze tudomásul kell vennem, hogy beleér a kezem a bilibe, és elfogadom, hogy erre nem egyhamar lesz igény annak ellenére, hogy potenciálisan hatalmas lehetőségeket látok benne. Az Ipar 4.0 előretörésével, a minőség ugyan javul, de a gyártási folyamatparaméterek figyelésére használt szenzorok alkalmazása gyakorlatilag kivette a minőségbiztosítás kezéből a gyártás minőségének felügyeletét. A minőségbiztosítási szakemberek nagy része a hagyományos mérőeszközökhöz ért, a modern technológia számukra ismeretlen terület. Ráadásul a statisztika és az adatelemzés területén is komoly lemaradásokkal küzdenek és az önképzés helyett inkább megmaradnak az egyszerű, de a kor követelményeinek már rég nem megfelelő módszerek alkalmazásánál. Noha néhány évvel ezelőtt az Ipar 4.0 mintájára valaki kitalálta a Quality 4.0 kifejezést, de sajnos ez már régen elkésett.
Források:
Robert L. Mason, John C. Young: Multivariate Statistical Process Control with Industrial Applications,
Society for Industrial and Applied Mathematics, American Statistical Association, 2002
S. Bersimis, S. Psarakis and J. Panaretos: Multivariate Statistical Process Control Charts: An Overview
Dr. Bill McNeese: Multivariate Control Charts: The Hotelling T2 Control Chart
https://www.spcforexcel.com/knowledge/variable-control-charts/hotelling-t2-control-chart
Pedro Villalbaa, Javier Sanchisb, Alberto Ferrera: A graphical user interface for PCA-based MSPC: a benchmark software for multivariate statistical process control in MATLAB, Chemometrics and Intelligent Laboratory Systems. 185:135-152.
https://doi.org/10.1016/j.chemolab.2018.12.004





