A különféle paraméteres vizsgálatok esetében előfeltétel az adataink eloszlásának ismerete. Persze, ha olyan szerencsések vagyunk, hogy a vizsgált adatsor normál eloszlású (Ne lógjon ki senki a sorból! - Miért fontos, hogy az adatok normál eloszlásúak-e?), akkor nincs különösebb okunk a fejfájásra. De mit tegyünk akkor, ha az adataink nem normál eloszlásúak? Hogyan tudjuk kitalálni, hogy vajon milyen eloszlást követnek az adatok és milyen paramétereket alkalmazva kapjuk meg azt az eloszlást, amely legalább megközelítőleg illeszkedik az adatainkra?

Nos, az R ebben is segít. Persze ez sem olyan egyszerű, mint amilyennek elsőre gondolnád, de azért nem is „rocket science”. Cseppet sem meglepő módon ehhez is kell egy csomag, ez esetben ezt úgy hívják, hogy ’fitdistrplus’. Pechünkre ez sajnos nem ugyanaz a csomag, mint az előző cikkben (Ne hanyagold el! - Normalitásvizsgálatok R-ben (Six Sigma in R)), de hát ez már csak ilyen… Szóval töltsük be ezt a kis csomagocskát.

Természetesen amennyiben ez a csomag még nincs feltelepítve az R-be, akkor a csomag az RStudio csomagtelepítőjével, vagy a

parancs segítségével is telepíthetjük.

A következő lépésben szükségünk lenne adatokra, amelyeket elemezni tudunk. Igazából most is választhatnék egy instant adatsort az R beépített adatsorai közül, de úgy gondoltam, hogy az érthetőség kedvéért inkább generálok különféle eloszlású adatsorokat, mert így jobban lehet majd látni, hogy mi történik akkor, ha mondjuk egy egyenletes eloszlású adatsorra egy normál eloszlású függvényt szeretnék ráhúzni. Szerencsére adott eloszlású véletlen adatok generálása nem túl nehéz R-ben, csak a vizsgálandó eloszlás tulajdonságait kell egy kicsit ismernünk. Például egy egyenletes eloszlású véletlen adatsort az

parancs begépelésével tudunk előállítani. A parancs segítségével létrehozunk egy 1000 véletlen számból álló adatsort és ezt elhelyezzük az ’uniadat’ változóba. A későbbiekben az ’uniadat’ változón keresztül tudunk majd hivatkozni az adatsorra. A ’runif()’ függvény első paramétere adja meg azt, hogy az adatsor hány elemből álljon, a második és a harmadik paraméter (a 0 és a 10) pedig megadja azt a számtartományt, ahonnan a véletlenszámokat ki kell választani. A változó nevének begépelésével meg tudjuk nézni a nyers adatokat is, de így ez nem sokat mond.

Egy egyszerű hisztogram véleményem szerint többet mond a generált adatokról. Ehhez a ’ggpubr’ csomagot is be kell töltenünk.

Ez az a csomag, aminek segítségével relatíve egyszerűen tudunk különféle diagramokat készíteni. Amint azt már korábban megtanultuk, a hisztogram létrehozásához meg kell adnunk azt, hogy hány csoportra osztjuk az adatainkat. Mivel fogok még más eloszlású adatsorokat is létrehozni, de mindegyikbe ezer darab adatot akarok generálni, ezért előre kiszámoltam az 1000 négyzetgyökét, amely kerekítve 32-re jött ki, vagyis akár hagyhatom is változatlanul az alapértelmezett 30-at, de meg is adhatom, hogy legyen a bin-ek száma 32, nagy különbséget nem fog jelenteni a dolog.

A létrehozott diagram így néz ki:

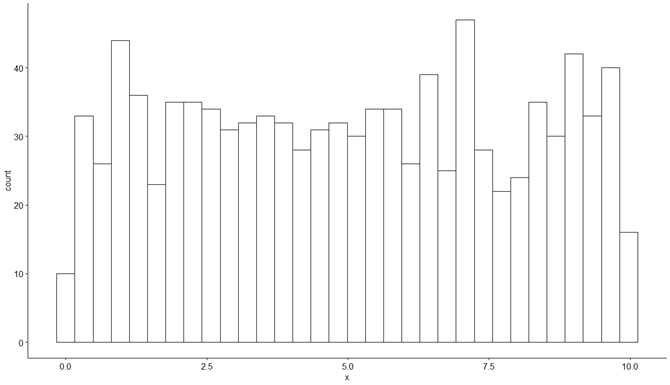
A hisztogramon látható, hogy az adatok nem túl pontosan, de hozzák a kért egyenletes eloszlást. Létre tudunk hozni ugyanígy normál eloszlású adatokat is.

Az ’rnorm()’ függvény a ’runif()’ függvényhez hasonlóan létrehoz egy 1000 elemből álló normál eloszlású adatsort, és ezt elhelyezi a ’normadat’ nevű változóban. A második sor pedig a fentiekhez hasonlóan megjeleníti a ’normadat’ adatsor hisztogramját.

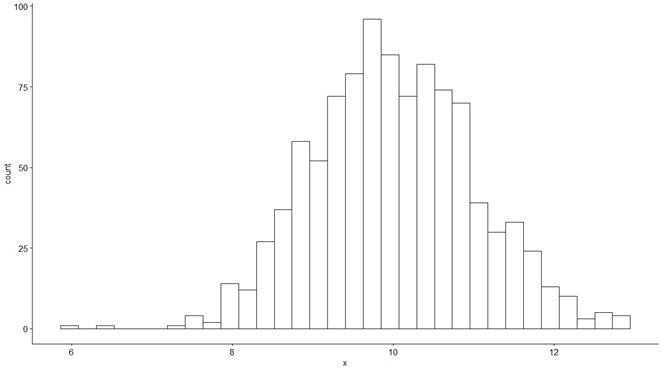
Hasonlóan létre tudunk hozni más eloszlású adatsorokat is:

Nem árt egy kis magyarázat a random függvények paramétereihez. A lognormális eloszlás esetében az ’rlnorm()’ függvény második és harmadik paramétere ugyanúgy az átlag és a szórás, hiszen ez nem más, mint egy normál eloszlás függvény logaritmus függvénye. Az exponenciális eloszlás és az ’rexp()’ függvény esetében a ’rate’ paraméter tulajdonképpen az exponenciális függvény Lambda (λ) paramétere. A weibull eloszlás esetében most csak két paramétert adtam meg, a ’shape’ paraméter (β) a görbe alakját, a ’scale’ paraméter (α) pedig a lapultságát adja meg. A harmadik paraméter (γ) az első két paraméter által megadott függvénygörbét tologatja az x-tengely mentén. A Khínégyzet-eloszlás, azaz a ’rchisq()’ függvény esetében csak a szabadsági fokok számát (df – degrees of freedom) kell kötelezően megadni.

Ezeket az eloszlásokat egy kicsit ötletszerűen válogattam ki, főleg amiatt, mert jórészt ezeket használtam eddig. Sajnos, ha ezeket ábrázolni akarom, akkor megint csak nem lesz elég a már eddig betöltött két csomag, szükségem van még egy további csomagra amiatt, hogy a különféle eloszlású adatsorok hisztogramjait egymás mellé tudjam helyezni. A csomag neve ’gridExtra’ és abban segít, hogy a ggplot2 diagramokat különféle módon el tudjuk rendezgetni egymás mellett.

Ismét érdemes vigyázni a kis-, és nagybetűkre. Ezután létrehozom az egyes adatsorok hisztogramjait és elmentem őket egy-egy változóba. Érdekes, hogy nemcsak számszerű értékeket vagy karaktersorokat, esetleg adatvektorokat, hanem diagramokat és más összetett objektumokat is el tudok menteni változóként és a változó nevével tudok hivatkozni rá.

A paraméterek között egy új paraméter is látható, ez a ’main’ paraméter. Ezzel címet lehet adni a diagramoknak, amely a diagram bal felső sarkában jelenik meg. Ezt még lehetne ciffrázni, de ebbe most nem szeretnék belemenni, mert a ’ggplot2’diagramoknak végtelen sok paramétere van, ez önmagában megérne egy külön cikket. Végül kirajzoltattam a hat diagramot egy 2 sorból és 3 oszlopból álló táblázatba. Ha ez megvan, akkor a ’gridExtra’ csomag ’grid.arrange()’ parancsa segítségével táblázatszerűen kirajzoltatom a hat hisztogramot.

A függvény egyszerűen használható, a zárójelben először megadom a kirajzolandó diagramok változóneveit abban a sorrendben, ahogy ki akarom őket rajzoltatni, majd megadom a sorok (nrow) és az oszlopok (ncol) számát. Bocs, de az eloszlások neveit utólag szerkesztettem rá az eredményre.

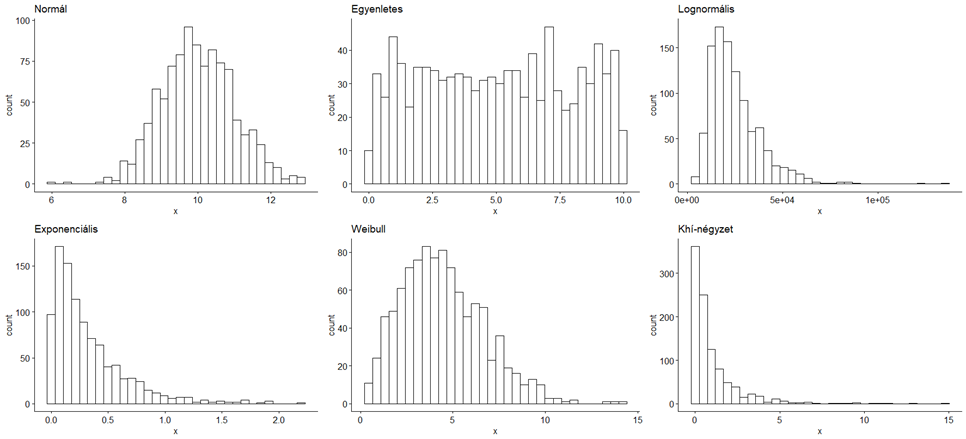
A különbség az adatsorok között szemmel látható, bár a lognormális, az exponenciális és a khí-négyzet eloszlások ezekkel a paraméterekkel eléggé hasonlítanak egymásra. Azonban ez eddig csak az előkészítés volt, az igazi kérdések most jönnek. Az adatsorra illeszkedő függvény meghatározása során két dolgot kell eldöntenünk.

• Melyik eloszlás típust tudjuk a legkisebb hibával ráfektetni az adatsorra?
• A kiválasztott eloszlásfüggvény milyen paraméterekkel fog a legjobban illeszkedni az adatsorra?

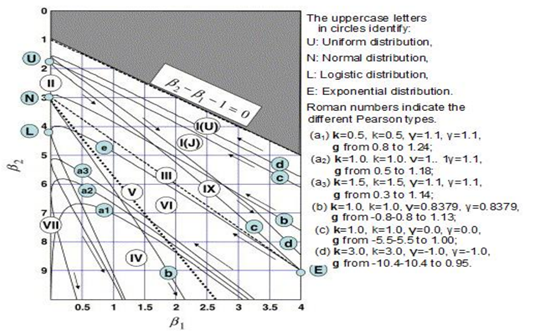
Az első kérdésre sajnos csak találgatással és próbálgatással tudunk felelni, … illetve ez azért mégsem teljesen igaz. A ’fitdistrplus’ csomag része a ’descdist()’ függvény, amely ad nekünk egyfajta támpontot arra vonatkozóan, hogy vajon melyik eloszlástípussal vagy típusokkal érdemes próbálkozni. Karl Pearson már 1895-ben kitalált egy olyan rendszert, amely alkalmazásával az adatsor elemeiből kiszámított két jellemző, a dőlés (skewness) négyzete és a lapultság (kurtosis) alapján tud adni egy közelítő támpontot az adatsor eloszlására vonatkozóan. A dőlésről és a lapultságról már részletesen írtam korábban (Értékelhető-e egy görbe alakja néhány együttható alapján?)

Ezt a módszert utána többen is továbbfejlesztették, így végül nem az eredeti Pearson által kidolgozott módszer, hanem két matematikus, Alison C. Cullen és H. Christopher Frey által 1999-ben publikált módszer került be a csomagba. Ennek részleteibe nem szeretnék belemenni, inkább nézzük meg egy-két példán keresztül, hogyan működik a gyakorlatban. Ehhez sorban meghívtam a fentebb említett ’descdist()’ függvényt az egyes adatsorokkal. Mivel a függvény azonnal meg is rajzolja az alább látható grafikonokat, ezért rögtön ki is rajzoltattam az alábbi összetett diagramot. Mivel a diagramok nem a ’ggplot2’, hanem az alap R-grafikai csomag segítségével készültek, ezért a diagramhálót másképpen kell létrehozni.

A ’par()’ függvény hozza létre a diagramhálót, a zárójelben lévő kicsit fura paraméter megadás segítségével lehet megmondani neki, hogy a diagramháló hány sorból és hány oszlopból álljon. Az ’mfrow = c(2, 3)’ kifejezésben az első szám adja meg a sorok, a második pedig az oszlopok számát. A ’descdist()’ függvénynek van egy fura paramétere ez a ’boot’. Ez amiatt kell, mert alapból a dőlés és a lapultság önmagukban nem igazán megbízható becsléseket adnak, ezért érdemes a bootstrap metódussal (ez egyfajta ismételt mintavételezés) az adatsorból mintákat venni és ezzel kiegészíteni a grafikont.   

A hat diagramon az x-tengelyen van a dőlés (skewness) négyzete, az y-tengelyen pedig a lapultság (kurtosis). A diagramokon megfigyelhetők nevezetes pontok és vonalak, amelyek a különféle eloszlás típusok helyét jelölik. A normál eloszlás helye például egy pont (lásd a bal felső diagramot), mert minden normál eloszlásra igaz, hogy a dőlése nulla (hiszen szimmetrikus), a lapultsága pedig három. Ha például eszembe jutott volna a t-eloszlást is iderángatni (A sörfőző, aki forradalmasította a statisztikát), akkor a t-eloszlásoknál a dőlés (skewness) szintén nulla, de a lapultság (kurtosis) kisebb, vagyis úgy tippelem, hogy a student-eloszlás valahová a normál és az egyenletes eloszlások közé esne. A diagramokan meg lehet figyelni, hogy az egyes eloszlások hol helyezkednek el a jellegzetes pontokhoz képest. A diagramok jobb felső részén található jelmagyarázatok eligazítanak a jellegzetes pontok között, így lehet némi benyomásunk arról, hogy az adatsorunk körülbelül milyen eloszlású lehet. A bootstrap által vett minták narancssárga színnel jelennek meg. Van olyan eloszlás, ahol ezeknek is egészen kicsi a szóródása, más eloszlásoknál ez sokkal nagyobb. A lognormális eloszlás esetében érdekes, hogy a bootstrap minták pontjai mennyire ráfekszenek a diagramon kijelölt görbe vonalra.

Még egyszer szeretném hangsúlyozni, hogy ennek a tesztnek a végeredménye nem egy konkrét döntés az adatsor eloszlásáról, csak egy indikáció, hogy merre érdemes keresgélni. Ráadásul a fenti példák esetében az eloszlások paraméterei teljesen önkényesen lettek kiválasztva. Érdemes sokat játszani a paraméterekkel, hogy vajon milyen paraméter kombináció esetében hová esnek a pontok a Cullen-Frey diagramon. Arról viszont, hogy konkrétan mi alapján lehet döntést hozni az adatsor eloszlásáról és hogyan lehet megállapítani az eloszlásfüggvény paramétereit majd a következő cikkben fogom részletesen ismertetni.

Források:

Marie Laure Delignette-Muller, Christophe Dutang: fitdistrplus: An R Package for Fitting Distributions, October 2014
http://www-eio.upc.edu/teaching/adtl/apunts/rstudio-eL1036.pdf

Vito Ricci: Fitting distributions with R, Release 0.4-21 February 2005
https://cran.r-project.org/doc/contrib/Ricci-distributions-en.pdf

Bachioua Lahcene: On Pearson families of distributions and its applications, African Journal of Mathematics and Computer Science Research, Vol. 6(5), pp. 108-117, May 2013
http://www.academicjournals.org/app/webroot/article/article1379928288_Lahcene.pdf

Karl Pearson: X. Contributions to the Mathematical Theory of Evolution. - JI. Skew Variation in Homogeneous Material, Philosophical Transactions of the Royal Society of London. A, Vol. 186 (1895), pp. 343-414
https://bayes.wustl.edu/Manual/Pearson_1895.pdf

Baptiste Auguie: Arranging multiple grobs on a page, 2017-09-09
https://cran.r-project.org/web/packages/gridExtra/vignettes/arrangeGrob.html