
A Nevada-chart-ról szóló bejegyzésben (A táblázat, amelynek olyan az alakja, mint Nevada államé – A Nevada-chart) már említettem, hogy ez a táblázat még több dologra is jó. Először is az alakja nem véletlenül olyan, mint amilyen. Egy kis összeadással még további hasznos információ morzsák is kinyerhetők a táblázat adataiból.
Például a táblázat adatait átlósan összeadva megkapjuk, hogy hány termék élte túl az 1 hónapot, a 2 hónapot, a három hónapot, és így tovább…

A pirossal jelölt cellák mutatják azokat a darabokat, amelyek 1 hónapig „éltek”, hiszen a júniusban gyártott 100 darabból már júliusban visszajött 3 darab, a júliusi 140-ből visszakaptunk 2 darabot augusztusban és hasonlóan az előbbiekhez az augusztusban gyártott 150 darabból már szeptemberben visszaküldtek 4 darabot. Ezeket összesítve azt mondhatjuk, hogy a június – augusztus időszakban gyártott 390 darabból 9 darab jött vissza egy hónap után. Hasonlóképpen értelmezhetők a sárga cellák, az ezekben található 7 darab két hónapig működött a gyártás után, illetve az egy szem zöld cellában található 5 darab 3 hónapig volt kinn a mezőn. Egy kicsit nagyobb méretű táblázat esetében azért ezt mókás összeadni táblázatkezelőben, de nem lehetetlen, a források között található egy link, ahol ékes angol nyelven részletesen le van írva a megfelelő tömbfüggvény alkalmazása.

Innen már csak egy kis képzelőerő kell ahhoz, hogy észrevegyük; az egy hónapig, két hónapig, három hónapig „túlélő” darabok tulajdonképpen egy gyakorisági hisztogramot alkotnak, amely a termékek „életgörbéjét”, illetve annak elejét jellemzik. Ha ennek a termékre jellemző gyakorisági eloszlásnak ismernénk a paramétereit, azaz rá tudnánk húzni az adatokra egy gyakorisági eloszlást, akkor ennek a függvénynek a felhasználásával meg tudnánk jósolni a következő néhány hónapban várható reklamált termékek mennyiségét!
A garanciális termékek élettartamának becslésére többféle eloszlást is szoktak alkalmazni, gyakran előforduló eloszlások (a teljesség igénye nélkül) az exponenciális eloszlás vagy a lognormális eloszlás, a gamma eloszlás, illetve ezek mindenféle változatai. Az egyik leggyakrabban alkalmazott eloszlástípus a Weibull-eloszlás; leginkább amiatt, mert ez az egyik legrugalmasabb eloszlástípus, nagyon sokféle tapasztalati görbére ráfektethető, illetve a fentebb felsorolt eloszlások egy része a Weibull-eloszlás speciális esetei.
A Weibull-eloszlást 1951-ben írta le Ernst Hjalmar Waloddi Weibull svéd mérnök, tudós és matematikus. A weibull-eloszlás azon a teórián alapul, hogy megbízhatósági szempontból egy rendszer elemei láncszerűen kapcsolódnak egymáshoz és a teljes rendszer élettartama megegyezik a rendszer leggyengébb láncszemének élettartamával.
Az adatsorunkra illeszkedő eloszlás meghatározása nem egyszerű feladat, talán ez az egyetlen olyan dolog, amelyet nem lehet egyszerűen táblázatkezelőben elvégezni, ehhez sajnos érdemes valamilyen speciális szoftvert alkalmazni. Én is ezt tettem és a Minitab szerencsére megadta, hogy a három adatpont pontosan követ egy kétparaméteres Weibull-eloszlást (jó, itt jöhet megint a kommentzápor, hogy mit akarok három adatpontból megállapítani, meg hogy nem illeszkednek a pontok eléggé az egyenesre):
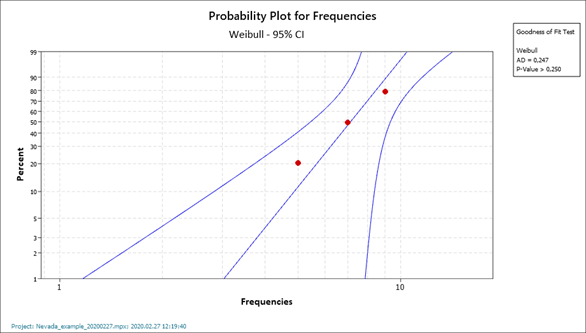

Maradjunk annyiban, hogy ez csak egy egyszerű példa. Szerencsére a program megadta a kétparaméteres weibull-eloszlás paramétereit is, így ezeket fel tudom használni majd a későbbiekben a jövőbeni darabszámok becslésére.
Következő lépésként meg kell határozni az úgynevezett cenzorált adatokat. Cenzorálásra akkor van szükség a statisztikában, amikor nem ismerjük a megfigyelt objektumok minden adatát. Jelen esetben például azt tudjuk, hogy egy hónap alatt 9, két hónap alatt 7 és három hónap alatt 5 termék ment tönkre, de a még piacon lévő termékek konkrét élettartamát nem ismerjük, csak azt tudjuk, hogy még nem mentek tönkre. Ezt hívjuk jobbra-cenzorálásnak.
Jelen esetben a cenzorált adatokat úgy kapjuk meg, hogy minden hónapban megnézzük, hogy még hány darab termék van a piacon az adott havi gyártásból, amely még nem ment tönkre. Ezt úgy kapjuk meg, hogy az adott hónapban gyártott mennyiségből kivonjuk az adott havi gyártásból reklamált termékeket. Jelen példánkban júniusban 100 darab terméket gyártottunk, amelyből eddig 3+3+5=11 darab terméket kaptunk vissza, így azon termékek mennyisége, amelyek már legalább három hónapja életben vannak, 100-11=89 darab. Ugyanez a júliusi gyártás esetében 140-2-4=134 darab, az augusztusban gyártott termékek esetében pedig 150-4=146 darab.
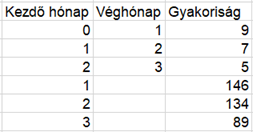
Vigyázzunk arra, hogy mit is jelentenek ezek a számok. A 89 darab az a mennyiség, amelyről már biztosan tudjuk, hogy túlélt már legalább 3 hónapot. A 134 darabról azt tudjuk, hogy túlélt már legalább két hónapot, a 146 darabról pedig azt tudjuk, hogy túlélt már legalább egy hónapot. Helyes a felvetés, ha valaki azt mondja, hogy a következő hónapban ezek az adatok már mások lesznek, ez tényleg egy pillanatkép, ami minden hónapban más és más képet fog mutatni.
A cenzorált adatokra később még szükségünk lesz, ezek segítségével fogjuk visszaszámolni a weibull-eloszlás által megadott valószínűségeket konkrét darabszámokra.
A következő feladat annak a kiszámítása, hogy a még a piacon lévő termékek hány százaléka fog megérni egy adott élettartamot, például a júniusban gyártott 100 darabból még a piacon lévő 89 darab esetében azt szeretnénk tudni, hogy hány termék fog visszajönni pontosan 4, pontosan 5 vagy pontosan 6 hónap múlva. Természetesen a júliusban gyártott darabok cenzorált mennyiségéből, azaz 134 darabból hány darab lesz reklamálva pontosan 3, pontosan 4 vagy pontosan 5 hónap múlva és persze az augusztusi 146 darab esetében is arra vagyunk kíváncsiak, hogy mennyi darab fog kiesni pontosan 2, pontosan 3, illetve pontosan 4 hónap múlva.
A Weibull-eloszlás esetében értelmezhető egy úgynevezett megbízhatósági függvény, amely azt fogja megmondani, hogy a termékek mekkora aránya fog túlélni egy megadott életkort, vagyis a fenti példával élve a júniusi 100 darabos gyártásból hány darab fog megérni több, mint 4 hónapot, több, mint 5 hónapot, illetve több, mint 6 hónapot. A megbízhatósági függvény a következőképpen néz ki:
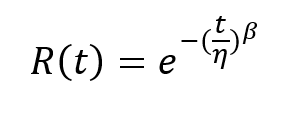
ahol
η – a weibull-eloszlás skála-paramétere (scale-parameter - fentebb 7,65113)
β – a weibull-eloszlás alak-paramétere (shape-parameter – fentebb 4,95200)
t – a termék élettartama hónapokban
Az R(t) függvény tulajdonképpen a kumulatív eloszlásfüggvény ellentettje (olyan, mintha a kumulatív eloszlásfüggvény értékeit kivonnánk 1-ből), vagyis ez is egy kumulatív (összegző) függvény, így néz ki:
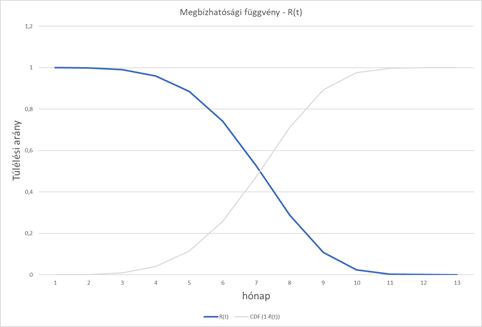
A függvényparaméterek ismeretében relatíve könnyen kiszámítható, hogy a piacon lévő termékek mekkora aránya fog túlélni 2, 3, 4, stb. hónapot, vagyis a termékek 99,9957945%-a fog túlélni 1 hónapot, 99,87%-a fog túlélni 2 hónapot, és így tovább…

A kumulatív eloszlásfüggvény esetében a három hónap alatt kiesett darabok száma tartalmazza az egy hónapon és a két hónapon belül meghibásodott darabok mennyiségét is. Egy kicsit kifordított logikával a megbízhatósági függvény esetében is igaz, hogy amelyik darab túlélt három hónapot, az túlélt egy hónapot és két hónapot is. Ezért, amikor az i-dik hónapot túlélt darabok arányát számoljuk, akkor el kell osztanunk R(ti)-t R(ti-1)-gyel, hogy megszüntessük a duplán, triplán, stb. számolt darabokat. Igen ám, de mi nem arra vagyunk kíváncsiak, hogy hány darab éli túl az i-dik hónapot, hanem arra, hogy hány esik ki i hónap után, vagyis a fentebb említett hányadost ki kell vonnunk 1-ből. Vagyis a képlet így néz ki:
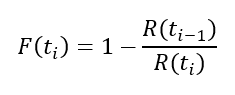
Azaz például a legalább két hónapot túlélt darabok esetében a kieső darabok aránya

Így, hogy végül megkaptuk a százalékos kiesési arányokat, már csak a havi kiesések becslése maradt hátra.

Kezdjük a júniusban gyártott darabok októberi kieséseinek becslésével. A júniusi gyártásból még 89 darab van kinn a piacon, és a megbízhatósági függvény alapján ezen 89 darab 3,0135 százaléka fog kiesni. Ez így 89*0,030135=2,68, azaz körülbelül 3 darabot jelent. Így az várható, hogy novemberben már csak 89-3, azaz 86 darab lesz a mezőn. A függvény alapján a 86 darab 7,8139 százaléka fog kiesni, így ez 82*0,078139=6,74 darabot jelent, azaz kb. 7 darab fog októberben és novemberben összesen kiesni, vagyis 4 darab jön hozzá az októberi 3-hoz. Decemberre várhatóan már csak 82 darab lesz ebből a tételből „életben”, de ezek 16,34 százaléka fog várhatóan meghibásodni, így az október – december időszakban 82*0,163411=13,00 darab fog várhatóan visszajönni, vagyis az előző kéthavi 7-hez még 6 darab fog hozzáadódni.
A júliusban gyártott mennyiség esetében a cenzorált 134 darab azt jelenti, hogy ennyi termék élt túl legalább 2 hónapot. Így az októberben várható kiesések kiszámításához azt a valószínűséget kell alkalmazni, amely a 3 hónap után kieső darabokra vonatkozik, ez esetben ez 0,008358, azaz 0,8358 százalék lesz. Így a júniusi tételből októberben 134*0,008358=1,12, azaz 1 darabot várunk.
A júliusi és az augusztusi becsült mennyiségeket végig kiszámolva megkapjuk a teljes havi becslést, amely azt mondja, hogy október végéig 4 darab, november végéig 12 darab, december végéig pedig összesen 28 darab reklamált termékünk lesz. Természetesen ezeket a számokat nem jóslatként, hanem becslésként kell kezelnünk, amelynek természetesen szintén van egy pontossága, amely persze szintén kiszámítható, de ezzel most nem terhelnélek téged sem és magamat sem.
Felhívom a figyelmet, hogy ez esetben még nem számoltunk azzal, hogy a következő hónapokban még további mennyiségeket fogunk gyártani és eladni, amelyek természetesen befolyásolják a várható kiesések mennyiségét. Egy másik fontos dolog, amire oda kell figyelni, hogy a weibull-eloszlás csak pozitív számok esetében működik, így ha az élettartam adatok között van nulla, akkor a weibull-eloszlás nem alkalmazható. Ilyenkor meg kell próbálni a már fentebb említett másfajta eloszlásokat alkalmazni, de ekkor természetesen a megbízhatósági függvény is más lesz.
Források:
Wikipédia – Weibull-eloszlás
https://hu.wikipedia.org/wiki/Weibull-eloszlás
Forecasting warranty returns
https://www.slideshare.net/TondaMacLeod/forecasting-warranty-returns-with-wiebull-fit
Sum up the diagonal of your data anywhere on a Sheet
http://excelunplugged.com/2016/01/26/sum-up-the-diagonal-of-your-data-anywhere-on-a-sheet/
Reliawiki - Warranty Data Analysis
http://reliawiki.org/index.php/Warranty_Data_Analysis





